Blogue de recherche vectorielle : apprentissage par renforcement basé sur des modèles pondéré par gradient de valeurs
23 juin 2022
23 juin 2022
23 juin 2022
Les blogues de recherche vectorielle offrent des explications courtes et non techniques des recherches révolutionnaires menées au sein de la communauté de recherche sur les vecteurs. Ils sont rédigés par des étudiants, postdoctorants, membres du corps professoral et affiliés de l’Institut Vector.
Claas Voelcker, Victor Liao, Animesh Garg, Amir-Massoud Farahmand
ICLR 2022 (article en vedette)
Avec l’essor de l’approximation puissante et flexible des fonctions, l’apprentissage par renforcement basé sur des modèles (MBRL) a gagné beaucoup de terrain ces dernières années. L’idée centrale du MBRL est intuitive : (a) utiliser les données obtenues lors de l’interaction en ligne d’un agent avec son environnement, (b) construire un modèle de substitution de cet environnement, et (c) utiliser ce modèle pour améliorer les capacités de planification de l’agent.

Légende : Un croquis de l’algorithme DYNA. Le modèle est utilisé pour générer des données supplémentaires pour l’entraînement des agents RL.
Bien qu’intuitive, cette approche peut souffrir lorsque nous obtenons des informations sensorielles multimodales à haute résolution. Dans ces cas, l’agent peut observer plus de monde que nécessaire pour accomplir sa tâche; Créer un modèle prédictif de l’environnement complet peut en fait être plus difficile que la tâche elle-même.
Dans la plupart des approches MBRL, le modèle environnemental est obtenu à partir de l’objectif de maximum de vraisemblance, souvent via une perte de reconstruction où le modèle tente de prédire la prochaine observation qu’un agent rencontre en se basant sur ses observations et actions précédentes. Cependant, si l’observation contient de nombreuses dimensions superflues, l’objectif MLE est inefficace, car une grande partie de la capacité du modèle est consacrée à l’approximation de la complexité totale de l’espace d’observation.
Notre proposition clé est de régulariser l’apprentissage du modèle selon la sensibilité de la fonction de valeur pour différentes entrées. Intuitivement, si la fonction de valeur n’est pas influencée par le changement d’observation, le modèle n’est pas nécessaire d’être précis.

Légende : Pour une tâche de conduite automobile, il est important de différencier les caractéristiques environnementales importantes des moins importantes. Bien qu’il soit très important de prédire la probabilité que des piétons entrent sur la route, les nuages dans le ciel ne sont que des distractions.
Ce phénomène a été appelé le « décalage d’objectifs » : le modèle ne sait rien de la tâche que l’agent tente de résoudre et aucune information de la tâche n’est renvoyée à l’apprentissage du modèle. Les objectifs de l’agent (« obtenir une récompense élevée ») et le modèle (« obtenir une faible erreur de reconstruction ») ne s’alignent pas nécessairement. En essayant de résoudre ce problème, on se heurte rapidement à un cercle vicieux : l’une des hypothèses fondamentales sous-jacentes à la prise de décision est que nous ne savons pas comment résoudre la tâche, sinon nous ne ferions pas d’apprentissage de modèles en premier lieu. Nous avons besoin d’un modèle précis de l’environnement avant de pouvoir résoudre la tâche, alors comment pouvons-nous renvoyer l’information de la tâche au modèle avant de la résoudre?

Légende : À gauche, les prédictions du modèle sont correctes. Du côté droit, ils ont tort. Dans l’image en haut à droite, la prédiction du modèle ne conduit pas à un changement dans la prédiction de la fonction valeur, donc aucune erreur n’est renvoyée. Dans le coin inférieur droit, l’erreur du modèle mène à une différence de fonction de valeur, donc l’erreur est propagée à l’algorithme RL.
Dans leurs articles « Value-aware model learning » et « Iterative value-aware model learning », Farahmand et al. présentent deux solutions potentielles au problème. En analysant la façon dont le modèle est utilisé dans un algorithme Dyna, ils montrent que le modèle n’influence la politique que par sa fonction de valeur. Cela signifie que même si la prédiction du modèle est erronée, tant que la prédiction de la fonction valeur correspond à l’environnement réel, l’agent RL n’est pas affecté par l’erreur du modèle. Inversement, même si le modèle ne fait qu’une petite erreur, si la fonction de valeur est très sensible à de petits changements dans l’espace d’états, la prédiction de valeur résultante peut être très erronée. À la suite de cette observation, Farahmand et al. proposent de remplacer la perte d’apprentissage du modèle par une perte qui mesure la différence de fonction de valeur.
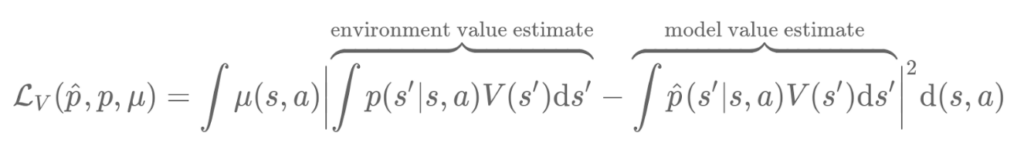
Bien que les fondements théoriques de l’approche VAML soient rigoureux, lorsqu’on applique naïvement l’algorithme en pratique, deux problèmes deviennent rapidement évidents.
(1) Dans de nombreux environnements RL, on ne peut pas supposer que l’espace d’états est pleinement exploré dans les premières itérations, ce qui signifie qu’il existe de nombreux états possibles dans lesquels nous n’avons pas de données pour apprendre une fonction de valeur. Cependant, un approximateur de fonction attribuera toujours une valeur à ces points, interpolant à partir de points déjà vus dans l’ensemble d’entraînement, ce qui donne souvent des valeurs incohérentes. Lorsque le modèle prédit qu’un état suivant se trouve dans une région inexplorée de l’espace d’états, la perte VAML ne le pénalisera pas pour avoir prédit un état complètement erroné si les fonctions de valeur s’alignent. Dans certains cas, elle peut même pousser la prédiction plus loin dans les régions inexplorées, simplement parce qu’elle cherche seulement à trouver un optimum local de la prédiction de la fonction valeur. Lorsque la fonction de valeur est mise à jour, les prédictions dans les régions de l’espace d’états qui ne sont pas couvertes par les données changent souvent rapidement, ce qui cause soudainement de très fortes erreurs de prédiction de fonction de valeur lors de l’utilisation des données du modèle.
(2) Le deuxième problème est la fluidité de la fonction de valeur et la perte VAML qui en résulte. Dans de nombreuses applications courantes, la fonction de valeur n’est ni convexe ni lisse, présentant des plateaux et des crêtes qui rendent la perte VAML difficile à optimiser. Dans l’image ci-dessous, nous montrons la fonction de valeur de l’environnement Pendule. La nature non lisse de la fonction se manifeste dans les deux crêtes nettes. Lorsque des fonctions de valeurs non lisses sont couplées à des estimations de valeurs hors distribution (problème #1), cela peut entraîner des normes de gradient massifs et la procédure subséquente de descente de gradient utilisant cette estimation peut diverger rapidement.

Légende : Une comparaison visuelle de toutes les fonctions de valeur discutées.
Pour résoudre le problème du désajustement du modèle sans introduire de nouveaux défis d’optimisation, nous soutenons qu’une bonne perte de modèle devrait avoir trois propriétés :
Notre point clé est d’inclure la fonction de valeur dans la perte comme mesure de la sensibilité des erreurs de modèle pour différents points de données et dimensions d’observation. Pour estimer cela, on calcule une approximation convexe de la fonction de valeur autour de chaque point de données en prenant son approximation de Taylor du premier ordre (au carré).
Cela nous donne une mesure de la sensibilité de la fonction de valeur aux distorsions dans l’espace d’états. Si le gradient de la fonction de valeur est faible dans une dimension spécifique, l’impact des erreurs de prédiction du modèle sera relativement faible. Inversement, dans les régions à forte pente, la prédiction de la fonction valeur change rapidement, donc le modèle devrait mesurer ces dimensions plus prudemment. En termes mathématiques, le gradient nous permet d’augmenter la perte L2 dans l’espace d’états par une régularisation locale dépendante de la fonction de valeur pour chaque point de données.

Nous appelons la fonction de perte le modèle pondéré valeur-GRadient (VaGraM).
La théorie sous-jacente à VaGraM et VAML nous dit qu’une fonction de perte alignée sur la valeur devrait être la plus importante dans les scénarios où le modèle est insuffisant pour capturer toute la complexité de l’environnement, ou dans les cas où il y a des dimensions non pertinentes dans l’espace d’états pour la tâche de contrôle. Pour vérifier que VaGraM augmente réellement la performance d’un algorithme RL basé sur des modèles de pointe, nous avons mené deux expériences principales :
(a) VaGraM aide-t-il quand le modèle ne convient pas?
Nous avons adopté l’environnement de contrôle DM populaire Hopper et l’optimisation des politiques basée sur modèle (MBPO). Nous avons remplacé la perte de MLE dans MBPO par VaGraM et diminué graduellement la taille du modèle pour limiter sa capacité. La performance de la solution de maximum vraisemblance s’est rapidement détériorée à mesure que le modèle diminuait, tandis que la performance de la version augmentée VaGraM est restée stable.

(b) VaGraM aide-t-il lorsque le modèle est difficile à ajuster à cause d’observations distrayantes?
Nous avons ajouté des dimensions superflues à l’espace d’états en suivant un système dynamique non linéaire indépendant. Cela s’est avéré être un environnement très exigeant, et MBPO et VaGraM ont rapidement perdu en performance avec un nombre croissant de dimensions distrayantes. Néanmoins, VaGraM a réussi à stabiliser le Hopper et à obtenir un certain mouvement vers l’avant face à 15 dimensions distrayantes, tandis que la solution MLE s’est effondrée sur la performance d’une politique aléatoire.

Dans d’autres expériences, nous avons constaté que VaGraM est capable de performer au même niveau que MBPO dans tous les environnements de contrôle DM, et même de le surpasser au benchmark Ant. Nous émettons l’hypothèse que l’espace d’états Ant n’est pas parfaitement ajusté pour le problème de contrôle, ce qui montre que les pertes conscientes de la tâche peuvent obtenir de meilleures performances même dans des environnements où auparavant nous ne nous attendions pas à ce que l’espace d’état et d’observation contienne des informations superflues.
Si vous voulez utiliser et étendre VaGraM, l’implémentation de la fonction de perte centrale est étonnamment facile et peut être intégrée dans la plupart des cadres d’apprentissage profond avec seulement un passage supplémentaire de rétropropagation à travers le réseau de fonctions de valeur.
Voici le code de la fonction de perte utilisant la bibliothèque jax :



